В 1904 г. Анри Пуанкаре предположил, что любой трехмерный объект, обладающий определенными свойствами трехмерной сферы, можно преобразовать в 3-сферу. На доказательство этой гипотезы ушло 99 лет. (Внимание! Трехмерная сфера – это не то, о чем вы подумали.) Российский математик Григорий Перельман доказал высказанную сто лет назад гипотезу Пуанкаре и завершил создание каталога форм трехмерных пространств.
Пуанкаре предположил, что 3-сфера уникальна и никакое другое компактное 3-многообразие (Некомпактные многообразия бесконечны или имеют края. Далее рассматриваются только компактные многообразия) не обладает теми свойствами, которые делают ее столь простой. У более сложных 3-многообразий есть границы, встающие как кирпичная стена, или множественные связи между некоторыми областями, похожие на лесную тропинку, которая то разветвляется, то снова соединяется. Любой трехмерный объект со свойствами 3-сферы можно преобразовать в нее саму, поэтому для топологов он представляется просто ее копией. Доказательство Перельмана также позволяет ответить на третий вопрос и провести классификацию всех существующих 3-многообразий.
Вам потребуется изрядное воображение, чтобы представить себе 3-сферу. К счастью, у нее много общего с 2-сферой, типичный пример которой – резина круглого воздушного шарика: она двухмерна, поскольку любая точка на ней задается всего двумя координатами – широтой и долготой. Если рассмотреть достаточно маленький ее участок под мощной лупой, то он покажется кусочком плоского листа. Крошечному насекомому, ползающему по воздушному шарику, он будет казаться плоской поверхностью. Но если козявка будет достаточно долго двигаться по прямой, то в конечном счете вернется в точку отправления. Точно так же 3-сферу размером с нашу Вселенную мы бы воспринимали как «обычное» трехмерное пространство. Пролетев достаточно далеко в любом направлении, мы бы в конце концов совершили «кругосветное путешествие» по ней и оказались бы в исходной точке.
Как вы уже догадались, n-мерная сфера называется n-сферой. Например, 1-сфера всем знакома: это просто окружность.
Математикам, доказывающим теоремы о многомерных пространствах, не приходится воображать себе объект изучения: они обращаются с абстрактными свойствами, руководствуясь интуитивными представлениями, основанными на аналогиях с меньшим числом измерений (к таким аналогиям нужно относиться с осторожностью и не принимать их буквально). Мы тоже будем рассматривать 3-сферу, исходя из свойств объектов с меньшим числом измерений.
1. Начнем с рассмотрения круга и ограничивающей его окружности. Для математиков круг – это двумерный шар, а окружность – одномерная сфера. Далее, шар любой размерности – это заполненный объект, напоминающий арбуз, а сфера – это его поверхность, больше похожая на воздушный шарик. Окружность одномерна, потому что положение точки на ней можно задать одним числом.
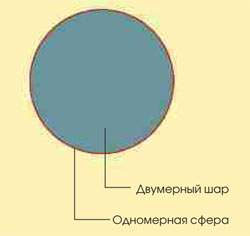
2. Из двух кругов мы можем построить двумерную сферу, превратив один из них в Северное полушарие, а другой – в Южное. Осталось склеить их, и 2-сфера готова.
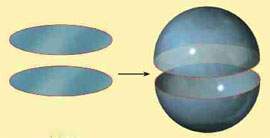
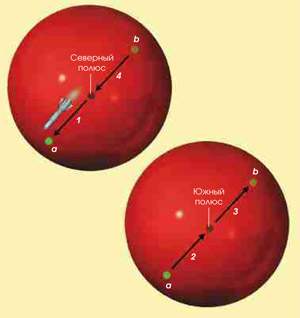
3. Представим себе муравья, ползущего с Северного полюса по большому кругу, образованному нулевым и 180-м меридианом (слева). Если мы отобразим его путь на два исходных круга (справа), то увидим, что насекомое движется по прямой линии (1) к краю северного круга (а), затем пересекает границу, попадает в соответствующую точку на южном круге и продолжает следовать по прямой линии (2 и 3). Затем муравей снова достигает края (b), переходит его и снова оказывается на северном круге, устремляясь к исходной точке – Северному полюсу (4). Заметьте, что во время кругосветного путешествия по 2-сфере направление движения сменяется на противоположное при переходе с одного круга на другой.
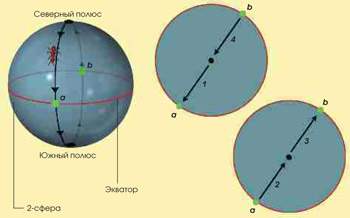
4. Теперь рассмотрим нашу 2-сферу и содержащийся в ней объем (трехмерный шар) и сделаем с ними то же самое, что с окружностью и кругом: возьмем две копии шара и склеим их границы вместе. Наглядно показать, как шары искажаются в четырех измерениях и превращаются в аналог полушарий, невозможно, да и не нужно. Достаточно знать, что соответствующие точки на поверхностях, т.е. 2-сферах, соединены между собой так же, как в случае с окружностями. Результат соединения двух шаров представляет собой 3-сферу – поверхность четырехмерного шара. (В четырех измерениях, где существуют 3-сфера и 4-шар, поверхность объекта трехмерна.) Назовем один шар северным полушарием, а другой – южным. По аналогии с кругами, полюса теперь находятся в центрах шаров.
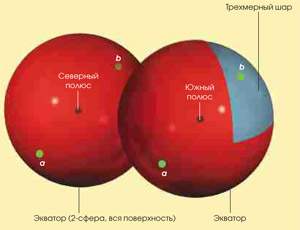
5. Вообразите, что рассмотренные шары – большие пустые области пространства. Допустим, из Северного полюса отправляется космонавт на ракете. Со временем он достигает экватора (1), которым теперь является сфера, окружающая северный шар. Пересекая ее, ракета попадает в южное полушарие и движется по прямой линии через его центр – Южный полюс – к противоположной стороне экватора (2 и 3). Там снова происходит переход в северное полушарие, и путешественник возвращается в Северный полюс, т.е. в исходную точку (4). Таков сценарий кругосветного путешествия по поверхности 4-мерного шара! Рассмотренная трехмерная сфера и есть то пространство, о котором идет речь в гипотезе Пуанкаре. Возможно, наша Вселенная представляет собой именно 3-сферу.
Рассуждения можно распространить на пять измерений и построить 4-сферу, но вообразить это чрезвычайно сложно. Если склеить два n-шара по окружающим их (n–1)-сферам, то получится n-сфера, ограничивающая (n+1)-шар.
Прошла половина столетия, прежде чем дело о гипотезе Пуанкаре сдвинулось с мертвой точки. В 60-х гг. XX в. математики доказали аналогичные ей утверждения для сфер пяти и более измерений. В каждом случае n-сфера действительно является единственным и простейшим n-многообразием. Как ни странно, получить результат для многомерных сфер оказалось легче, чем для 3- и 4-сферы. Доказательство для четырех измерений появилось в 1982 г. И только исходная гипотеза Пуанкаре о 3-сфере оставалась неподтвержденной.
Решающий шаг был сделан в ноябре 2002 г., когда Григорий Перельман, математик из Санкт-Петербургского отделения математического института им. Стеклова, отправил статью на сайт www.arxiv.org, где физики и математики со всего мира обсуждают результаты своей научной деятельности. Топологи сразу уловили связь работы российского ученого с гипотезой Пуанкаре, хотя напрямую автор ее не упомянул.
На самом деле доказательство Перельмана, правильность которого еще никому не удалось поставить под сомнение, решает гораздо более широкий круг вопросов, чем собственно гипотеза Пуанкаре. Предложенная Уильямом Терстоном (William P. Thurston) из Корнеллского университета процедура геометризации позволяет провести полную классификацию 3-многообразий, в основу которой положена 3-сфера, уникальная в своей возвышенной простоте. Если бы гипотеза Пуанкаре была ложной, т.е. существовало бы множество пространств столь же простых, как сфера, то классификация 3-многообразий превратилась бы в нечто бесконечно более сложное. Благодаря Перельману и Терстону у нас появился полный каталог всех допускаемых математикой форм трехмерного пространства, которые могла бы принять наша Вселенная (если рассматривать только пространство без времени).
Чтобы глубже понять гипотезу Пуанкаре и доказательство Перельмана, следует поближе познакомиться с топологией. В этом разделе математики форма объекта не имеет значения, как будто он сделан из теста, которое можно как угодно растягивать, сжимать и изгибать. Зачем же нам задумываться о вещах или пространствах из воображаемого теста? Дело в том, что точная форма объекта – расстояние между всеми его точками – относится к структурному уровню, который называют геометрией. Рассматривая объект из теста, топологи выявляют его фундаментальные свойства, не зависящие от геометрической структуры. Изучение топологии похоже на поиск наиболее общих черт, присущих людям, методом рассмотрения «пластилинового человека», которого можно превратить в любого конкретного индивида.
В популярной литературе часто встречается избитое утверждение, что с точки зрения топологии чашка ничем не отличается от бублика. Дело в том, что чашку из теста можно превратить в бублик, просто сминая материал, т.е. ничего не слепляя и не проделывая отверстий. С другой стороны, чтобы сделать бублик из шара, в нем непременно нужно сделать дырку или раскатать его в цилиндр и слепить концы, поэтому шар – это совсем не бублик.
Топологов больше всего интересуют поверхности шара и бублика. Поэтому вместо сплошных тел следует представлять себе воздушные шарики. Их топология по-прежнему различна, поскольку сферический воздушный шарик невозможно преобразовать в кольцевой, который называется тором. Сначала ученые решили разобраться, сколько вообще существует объектов с различной топологией и как их можно охарактеризовать. Для 2-многообразий, которые мы привыкли называть поверхностями, ответ изящен и прост: все определяется количеством «дырок» или, что то же самое, количеством ручек. К концу XIX в. математики поняли, как классифицировать поверхности, и установили, что самая простая из них – сфера. Естественно, топологи начали задумываться о трехмерных многообразиях: уникальна ли 3-сфера в своей простоте? Вековая история поисков ответа полна неверных шагов и ошибочных доказательств.
Анри Пуанкаре вплотную занялся этим вопросом. Он был одним из двух сильнейших математиков начала XX в. (другим был Давид Гильберт). Его называли последним универсалом – он успешно работал во всех разделах как чистой, так и прикладной математики. Кроме того, Пуанкаре внес огромный вклад в развитие небесной механики, теорию электромагнетизма, а также в философию науки, о которой написал несколько популярных книг.
Пуанкаре стал основателем алгебраической топологии и, используя ее методы, в 1900 г. сформулировал топологическую характеристику объекта, названную гомотопией. Чтобы определить гомотопию многообразия, нужно мысленно погрузить в него замкнутую петлю. Затем следует выяснить, всегда ли можно стянуть петлю в точку, перемещая ее внутри многообразия. Для тора ответ будет отрицательным: если расположить петлю по окружности тора, то стянуть ее в точку не удастся, т.к. будет мешать «дырка» бублика. Гомотопия – это количество различных путей, которые могут воспрепятствовать стягиванию петли.
На n-сфере любую, даже замысловато закрученную петлю всегда можно распутать и стянуть в точку. (Петле разрешается проходить через саму себя.) Пуанкаре предполагал, что 3-сфера – единственное 3-многообразие, на котором в точку можно стянуть любую петлю. К сожалению, он так и не смог доказать свое предположение, которое впоследствии стали называть гипотезой Пуанкаре.
Проведенный Перельманом анализ 3-многообразий тесно связан с процедурой геометризации. Геометрия имеет дело с фактической формой объектов и многообразий, сделанных уже не из теста, а из керамики. Например, чашка и бублик геометрически различны, поскольку их поверхности изогнуты по-разному. Говорят, что чашка и бублик – два примера топологического тора, которому приданы разные геометрические формы.
Чтобы понять, зачем Перельман использовал геометризацию, рассмотрим классификацию 2-многообразий. Каждой топологической поверхности назначена уникальная геометрия, искривление которой распределено по многообразию равномерно. Например, для сферы – это идеально сферическая поверхность. Другая возможная геометрия для топологической сферы – яйцо, но его кривизна не везде распределена равномерно: острый конец изогнут сильнее, чем тупой.
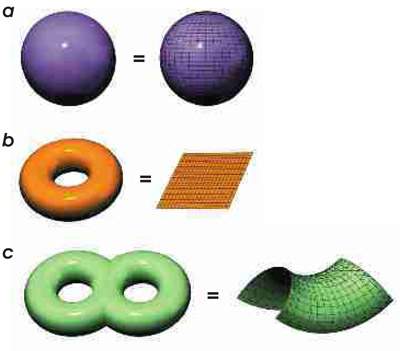
2-многообразия образуют три геометрических типа. Сфера характеризуется положительной кривизной. Геометризированный тор – плоский, ему свойственна нулевая кривизна. Все остальные 2-многообразия с двумя или более «дырками» имеют отрицательную кривизну. Им соответствует поверхность, похожая на седло, которое спереди и сзади изгибается вверх, а слева и справа –вниз. Такую геометрическую классификацию (геометризацию) 2-многообразий Пуанкаре разработал вместе с Паулем Кебе (Paul Koebe) и Феликсом Клейном (Felix Klein), именем которого названа бутылка Клейна.
Возникает естественное желание применить подобный метод к 3-многообразиям. Можно ли найти для каждого из них такую уникальную конфигурацию, у которой кривизна была бы распределена равномерно по всему многообразию?
Оказалось, что 3-многообразия гораздо сложнее своих двумерных собратьев и большинству из них нельзя поставить в соответствие однородную геометрию. Их следует разделять на части, которым соответствует одна из восьми канонических геометрий. Данная процедура напоминает разложение числа на простые множители.
Каким же образом можно геометризировать многообразие и придать ему повсюду равномерное искривление? Нужно взять некую произвольную геометрию с различными выступами и углублениями, а затем сгладить все неровности. В начале 90-х гг. XX в. к анализу 3-многообразий приступил Гамильтон, который воспользовался уравнением потока Риччи, названным так в честь математика Грегорио Риччи-Курбастро (Gregorio Ricci-Curbastro). Оно в чем-то схоже с уравнением теплопроводности, которое описывает тепловые потоки, протекающие в неравномерно нагретом теле до тех пор, пока его температура не станет везде одинаковой. Точно так же уравнение потока Риччи задает такое изменение кривизны многообразия, которое ведет к выравниванию всех выступов и углублений. Например, если начать с яйца, то оно постепенно станет сферическим.
Перельман добавил к уравнению потока Риччи новый член. Внесенное изменение не устранило проблему особенностей, но позволило провести гораздо более глубокий анализ. Российский ученый показал, что над многообразием в виде гантели можно провести «хирургическую» операцию: отрезать тонкую трубку по обе стороны от появляющегося пережима и заделать торчащие из шаров открытые трубки сферическими колпачками. Затем следует продолжать изменение «прооперированного» многообразия в соответствии с уравнением потока Риччи, а ко всем возникающим пережимам применять вышеописанную процедуру. Перельман также показал, что сигарообразные особенности появляться не могут. Таким образом, любое 3-многообразие можно свести к набору частей с однородной геометрией.
Когда поток Риччи и «хирургическую операцию» применяют ко всем возможным 3-многообразиям, любое из них, если оно столь же простое, как 3-сфера (иначе говоря, характеризуется такой же гомотопией), обязательно сводится к той же самой однородной геометрии, что и 3-сфера. Значит, с топологической точки зрения, рассматриваемое многообразие и есть 3-сфера. Таким образом, 3-сфера уникальна.
Ценность статей Перельмана заключается не только в доказательстве гипотезы Пуанкаре, но и в новых методах анализа. Ученые всего мира уже используют в своих работах результаты, полученные российским математиком, и применяют разработанные им методы в других областях. Оказалось, что поток Риччи связан с так называемой группой перенормировки, которая определяет, как изменяется сила взаимодействий в зависимости от энергии столкновения частиц. Например, при низких энергиях сила электромагнитного взаимодействия характеризуется числом 0,0073 (приблизительно 1/137). Однако когда два электрона сталкиваются лоб в лоб при скорости, почти равной скорости света, значение этой силы приближается к 0,0078. Математика, описывающая изменение физических сил, очень похожа на математику, описывающую геометризацию многообразия.
Увеличение энергии столкновения эквивалентно изучению силы на меньших расстояниях. Поэтому группа перенормировки подобна микроскопу с изменяемым коэффициентом увеличения, который позволяет исследовать процесс на разных уровнях детализации. Точно так же поток Риччи представляет собой микроскоп для рассмотрения многообразий. Выступы и углубления, видимые при одном увеличении, исчезают при другом. Вполне вероятно, что в масштабах длины Планка (около 10-35м) пространство, в котором мы живем, выглядит как пена со сложной топологической структурой. Кроме того, уравнения общей теории относительности, которые описывают характеристики гравитации и крупномасштабной структуры Вселенной, тесно связаны с уравнением потока Риччи. Как это ни парадоксально, член, добавленный Перельманом к выражению, которое использовал Гамильтон, возникает в теории струн, претендующей на звание квантовой теории гравитации. Не исключено, что в статьях российского математика ученые найдут еще много полезной информации не только об абстрактных 3-многообразиях, но также и о пространстве, в котором мы живем.
По материалам: Современная космология.